Friday, 9 July 2010
2D Dynamic Lighting - well almost
Some of the effects remind me of binary star systems. Here are 2 more apps showing real time moving light sources with various effects:
Monday, 28 June 2010
Physics Evolution: Step 1
So I've been getting to grips with the engine which seems fairly simple to use and here is a little demo:
So what is next? The idea behind genetic algorithms is that some genotype, in this case a string of 1's and 0's, determines a phenotype, in this case the structure of a creature. By randomly mutating bits in the genetic code, and testing the resulting creatures against one another, and sticking with the code that yields the best results, creatures can be made to evolve. Creatures can for example be tested for their ability to run fast, or for their ability to jump, or to swim.
Ideally I will reach a stage where code can be saved at any stage of the process, and can be emailed to another person somewhere else in the world who can continue to evolve the same creature. Obviously since evolution is random there could be some very interesting splits. It would be nice to create a sandpit where creatures could be watched. A further investigation would be the effect of mating genotypes to create hybrid creatures, and obviously the nature of the algorithm used to produce creature structure would determine the success of this.
Anyway stay tuned for progress!
Monday, 31 May 2010
Galaxy
Just click the two images below to launch the 2D and 3D simulations! Enjoy.
The three examples below show that with slightly different initial conditions, the shapes we find in a simple galactic simulation like this one, are actually surprisingly similar to those we see in real galaxies, for example in the first you can almost see the emergence of the spiral arms of our own galaxy the Milky Way.
Saturday, 15 May 2010
Attempt at "fast" solution to the N-Body Problem
 Lets first take a look at the example in its simplest form, with just two bodies. The two bodies pull on each other by the gravitational force, which causes both to accelerate along a vector pointed along the line joining them. This is a very simple problem to solve and any university level physicist should find solving it trivial. In the case of more bodies however, an analytical solution becomes extremely complicated and far beyond the reach of my mathematical understanding; but what I do understand is computers and iterative techniques. The simplest way therefore to solve a problem with more than two bodies would be simply to summate the forces of all the bodies acting on one body at a given moment in time and update its velocity, then repeat this for each of the other bodies in your system.
Lets first take a look at the example in its simplest form, with just two bodies. The two bodies pull on each other by the gravitational force, which causes both to accelerate along a vector pointed along the line joining them. This is a very simple problem to solve and any university level physicist should find solving it trivial. In the case of more bodies however, an analytical solution becomes extremely complicated and far beyond the reach of my mathematical understanding; but what I do understand is computers and iterative techniques. The simplest way therefore to solve a problem with more than two bodies would be simply to summate the forces of all the bodies acting on one body at a given moment in time and update its velocity, then repeat this for each of the other bodies in your system.Obviously for a number of bodies N, the number of force checks that would have to be done would increase very quickly, in fact at a rate N*N, which means for 1000 bodies, 1 million checks would have to be carried out, remember this is per instant in time.
 I propose a solution that uses the bitmap functionality in flash, along with the blur filter. I am sure that it won't stand up to rigorous mathematical scrutiny, but from an aesthetic standpoint, it does the job near enough ok.
I propose a solution that uses the bitmap functionality in flash, along with the blur filter. I am sure that it won't stand up to rigorous mathematical scrutiny, but from an aesthetic standpoint, it does the job near enough ok.The idea is that each body is represented by a pixel, with a colour related to its mass. By applying a blur filter on the bitmap, the gravitational field of the pixel is extended into the surrounding region. A brighter region means more gravitational force, and a darker region less. To solve the problem particles simply need to be accelerated along the line of highest gradient towards brighter regions. This way only N checks have to be carried out massively decreasing computing time.
For example carrying out the test with 10,000 particles, which would otherwise kill my computer (at 24 frames per second that would be 2,400,000,000 force checks per second!) it actual runs reasonably well!
Anyway take a look and feel free to make suggestions to improve the model. Just click the first image to launch the simulation!
Note: Limitations of the simulation include -
- Blur is not complete, i.e gravity has a limited range - this may be analogous to simulations of the large scale universe where distances are two large for information to pass between.
- Blur takes multiple steps to update (slow information rate)
- Singularities such as collisions cause erratic behaviour (sudden velocity boosts)
Wednesday, 30 December 2009
How To Build A Raytracer: Part II
The Camera
To start with lets create a camera at a position in space [camX,camY,camZ]. This camera can move up, down, left, right, in and out around your scene, and is where all of the initial rays are fired from. The image below shows how the rays exit the camera through the scene. It is clear that we want our rays to pass from the camera through the image, as shown in this diagram, but how do we find these rays! For a horizontal camera with no rotational properties this is actually very easy, so lets take a look at how to do it.
 Traditionally cameras have a property called the field of view. This is related to the range of angles that a camera can see. A fisheye lens, for example, has a large field of view (180 degrees?). High field of views can result in image curving and I've found that the optimum angle between the horizontal and the top vertical for ray tracing is around π/6 degrees giving a field of view of π/3 or 60 degrees.
Traditionally cameras have a property called the field of view. This is related to the range of angles that a camera can see. A fisheye lens, for example, has a large field of view (180 degrees?). High field of views can result in image curving and I've found that the optimum angle between the horizontal and the top vertical for ray tracing is around π/6 degrees giving a field of view of π/3 or 60 degrees.Once we've decided on a field of view for our ray tracer we can determine the distance between the image plane and the camera. Remember, unless the image is completely square the field of view in the vertical range and the horizontal range will be different. Programmatically, creating a new variable called the scale of view makes things far easier where:
var scaleX:Number = Math.tan(fovX);
var scaleY:Number = Math.tan(fovY/(scenewidth/sceneheight));
In the above actionscript, scene width and scene height are the pixel height and width of the image you want to create. Once we have our scales of view we can start firing rays. In a ray tracer rays are fired through every single pixel in the image. Although it results in pixel perfect images the computation required can also be rather large for high resolutions. This is why ray tracers are not currently used in real time applications.
So the next step in the ray tracing algorithm is to cycle through each pixel creating rays. I suggest using two embedded for loops although there are other ways of doing this depending on the structure of your program:
for(var i:int = 0; i < scenewidth; i++)
{
for(var j:int = 0; j
{
rayX = scaleX*(2*i-scenewidth)/scenewidth;
rayY = scaleY*(2*j-sceneheight)/sceneheight;
rayZ = 1;
// After we have created the ray we calculate collisions - and then render the pixel
}
}
The above is a simple example of creating all the rays needed for a scene.
In vector mathematics a lot of calculations rely on the vector being unitary (meaning of length 1). To fix this just take the modulus of (rayX, rayY, rayZ) and divide each of rayX, rayY, and rayZ by this modulus.
This simple model can be extended by adding yaw and pitch, and for the really enthusiastic even roll! These are 3 types of rotation. The simplest way to create rotations is to rotate the ray vectors around the camera's location once they have been generated using matrix transforms. This will fit into a later tutorial.
Stay tuned for the next in the series soon!
How To Build A Raytracer: Part I
 This is not just source code that I'm posting up, I will describe everything that I feel is needed to build a ray tracing engine without necessarily giving too much code. In the end I feel this is a far more rewarding way of learning flash and creating new projects, and is how I have taught myself in the past. Certain aspects of maths throughout the tutorial may be of a reasonable level but most high school vector course books should give enough knowhow to be able to see what is going on. So lets begin.
This is not just source code that I'm posting up, I will describe everything that I feel is needed to build a ray tracing engine without necessarily giving too much code. In the end I feel this is a far more rewarding way of learning flash and creating new projects, and is how I have taught myself in the past. Certain aspects of maths throughout the tutorial may be of a reasonable level but most high school vector course books should give enough knowhow to be able to see what is going on. So lets begin.Note: the image to the right shows the kinds of lighting effects a raytracer can produce.
What is a raytracer
In nature a ray of light travels from a light source - interacts with some objects and either disappears into space or reaches our eyes. What we see depends on what the ray has collided with on the way to our eye. For example taking a light source to be the sun, trillions of rays hit earth every second, each of these reflects, refracts and is absorbed by trees, by roads, by cars and by other people. For us, the onlookers, only a tiny fraction of these rays hit our eyes, but when they do, the individual rays (photons) create the scene we see in front of us on the back of our eyes ready for our brains to untangle and interpret.
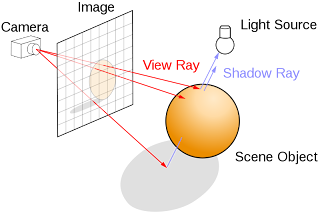
The idea of a raytracer - at least in the sense of this tutorial - takes what happens in nature and reverses all of the processes. Rays are created in the back of our eyes and are fired in a range of directions at our scene. Each ray passes through a point in our image and will either pass through our scene or hit an object. The image to the left helped me understand the ray firing process. When a ray hits an object there are 3 possibilities:
(i) The ray absorbs the ray
(ii) The ray reflects the ray
(iii) The ray refracts the ray
In the first case, a new ray is case from the point where the ray scene collision occurred, in the direction of any light sources in the scene. If there are no objects in the way then the object is lit, otherwise the object is in shadow.
In the second case a new ray can be cast depending on the surface normal of the object which can interact with the scene again. The ray can keep colliding with objects up to an arbitrary number of times so theoretically a ray could bounce between objects forever.
In the third case a new ray can be cast depending on the surface normal and refractive index of the material. As above this ray can continue to interact with the scene.
These three cases are not mutually exclusive. In a scene there can be any amount of refraction, refraction, absorption and shadowing, which gives ray tracers their realism. Take a look at the top image for examples of all three, and the image by pixar below is another example.
We've seen that a raytracer is just a way to render a scene which is physically realistic and can produce effects like shadowing, reflection and refraction in a far simpler way than many other rendering methods.
In my next post I'll explain how the camera works and how to set up our first scene.
My Fluid Dynamics Engine in AS3
Jos Stam's article on fluid dynamics for games started it all, having a similar effect on this area of research as Thomas Jakobsen's article had on the use of Verlet Integration in physics engines. The beauty of the fluid solver is that it provides a computationally quick and stable approach to simulation of fluid dynamics, which can be easily expanded into 3 dimensions and used to solve many more advanced problems.
Eugene Zatepyakin was the next step in the chain creating a fast engine in AS3 which I talked about in a previous post. I decided to write my own version of the engine and here it is:
The first example shows 4000 particles floating around in the simulated fluid - just click on it to launch to flash file - once it is running click and drag to make the fluid move.

Sunday, 8 November 2009
String Thing

Friday, 23 October 2009
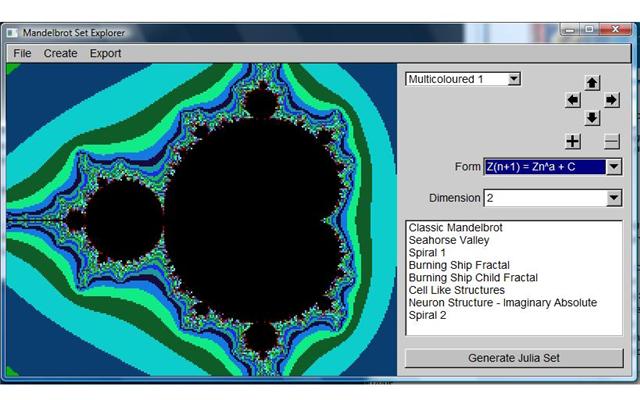
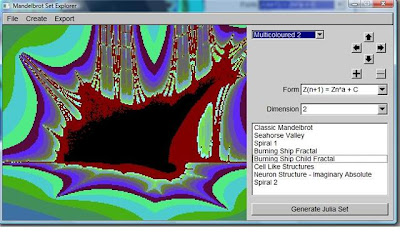
Mandelbrot Explorer
Here are a few screen shots and an outputted jPeg file. The program is capable of producing high resolution "deep zoom" images of 1200 by 800 pixels. These can look amazing. It handles powers of the mandelbrot set, as well as different forms - including the amazing "Burning Ship" fractal.
The Program is free of charge to anyone who wants it. Just send me a note and I'll provide download links! Enjoy the beauty of mathematics.
Wednesday, 21 October 2009
Strange Attractors - Drawing the universe
The mandelbrot is a fractal set, so I thought it might be interesting to look at some other fractal sets. Below is a representation of a Strange Attractor - technically a system with chaotic dynamics and a non-integer dimension. The whole program was written in just a few lines of code and it is actually fairly straight forward to work out, just like the Mandelbrot set, but the results are spectacular. It really does seem like the universe is being drawn out in front of you - and it is true that a lot of the patterns found in fractal mathematics do appear in the structures of macroscopic objects, for example in the spiral arms of galaxies, or in nebula cloud formation.
Monday, 5 October 2009
Fluid Dynamics using AS3
 As a physicist I find things like this incredible. Fluids are extremely complex mathematically, so when I came across Eugine Zatepuakin's work on fluid dynamics I was amazed by the speed and accuracy of the simulations!
As a physicist I find things like this incredible. Fluids are extremely complex mathematically, so when I came across Eugine Zatepuakin's work on fluid dynamics I was amazed by the speed and accuracy of the simulations! Just click the right image for a full preview, you'll be blown away! When I've got a bit more time I'll write a thread explaining how fluid dynamics simulations work, and explain the basic principles of coding something like this in flash, but for now check it out!
Just click the right image for a full preview, you'll be blown away! When I've got a bit more time I'll write a thread explaining how fluid dynamics simulations work, and explain the basic principles of coding something like this in flash, but for now check it out!Move your mouse around to create dense regions and click to change the rendering mode. I love that flash is capable of handling these kinds of calculations. I remember playing a game called plasma pong which used very similar fluid dynamics to Eugine's model. Unfortunately the game is no longer available for download because pong is a trademark of Atari but here is a nice little video of the game in action.
Here is a little youtube clip of the game, just click to launch it! :)
Enjoy!
Wednesday, 30 September 2009
Fractals And The Mandelbrot Set In Nature!
Anyway, I just had a browse to see what kinds of examples I could find of fractals present in nature and some of the images I found were unbelievable! Just check out some of the images below (click for full size). I find the images of rivers and streams are the closest in appearance to the Mandelbrot set, although some other patterns are also found, like the spiral shape of the tornado.

More Emergence - The Mandelbrot Set
The rules that govern the Mandelbrot set are very simple - anyone with a basic understanding of complex number theory should be able to make it work. Understanding why, and how it works is a much harder question, and something that I won't go into. I'm just here to make some pretty pictures!
So how does the mandelbrot set work? Imagine the image to the right is made up of points, set co-ordinates. Each point is described by one number which tells us where it lies vertically, and another which tells us where it lies horizontally. Mandelbrot mapped the vertical location to imaginary space, and the horizontal location to real space - in other words he mapped the co-ordinates to complex space (for mathematicians out there - a pixel is pretty much equivalent to a point on an Argand diagram).
Complex space is made up of complex numbers of the form a + ib, where a and b are both real numbers.
We can calculate the square of a complex number using:
(a + ib).(a + ib) = a*a - b*b + 2iab
The real component of the new number is now (a*a-b*b), and the imaginary component is 2ab.
The Mandelbrot set arrises when the number of iterations for the value of a*a+b*b is calculated to be greater than some threshold value for each pixel. The colour variation you see on the diagram depends on the number of iterations for the prior calculation for that particular starting number.
For lower iterations the detail in the image does not appear as much. Where as for higher iterations (the demo below is set to 500 iterations per pixel) the detail achieved will be far greater.
One issue arrises in the way that computers - in this case flash - handles numbers. Floating point numbers will not achieve the required accuracy when the amount of zoom on the graph is too high. Unfortunately this results in an infinite amount of zoom being impossible on this platform.
Just click on the image to the right to launch the mandelbrot set program. Enjoy it, and have a play around going down several routes. To the left of the main cardioid bulb is a region dubbed seahorse valley. It is one of my favourites!
For some more interesting articles on the Mandelbrot Set and some incredible zooms visit:
University of Utah
Mandelbrotset.net
Enjoy!
Monday, 14 September 2009
Build your own color detector.

Understanding the nature of the colours present in light is a vital part of this project. Light has an additive nature, unlike pigments, which have a subtractive nature. This means that increasing proportions of red, green, and blue light result in
the formation of white light, and various combinations of those colours can form every colour in the visible spectrum.
Due to their ability to produce such a vast array of hues they also form the basis for colour formation in standard computer monitors, televisions and other liquid crystal displays. Technically the choice of red, green and blue are not exact, they are chosen due in large part to the sensitivities of the cone cells in the rear of the retina. Differences in the hues of the red, green and blue constituents chosen may produce different absolute colour spaces, for example sRGB and Apple RGB are two absolute colour spaces used in computer monitors. In computing terms the R, G, B value of a colour represents its red, green and blue components proportionally, normally each on a scale of 0-255 (This requires three 8-bit values). For various other purposes in computer graphics a further two bits per unit may be added, for example RGBA includes information about the alpha channel (transparency) of a pixel, and contains three 10-bit units of colour per pixel. In the case of visible light however only the RGB values, and their associated intensities need to be taken into account.
Since the LDRs that will be used in the colour detector have little or no wavelength dependence it is necessary to use colour filters to determine which wavelengths of light are hitting which detector and in what proportions. Colour filters work by transmitting certain wavelengths of light and reflecting or destroying through interference, the other wavelengths. Manufacturers often produce filters that allow not only the target colours wavelengths through. The effect of this is is often to brighten up the filters, by letting through more light.
A problem with this is that it is practically impossible to determine the exact chromaticities of the filter. A solution to this involves measuring intensities of pure red, green and blue light after they pass through the filter when compared to the intensities before transmission. By creating a transformation matrix from one set of colours to the other and inverting that matrix, a transform will be created to convert measured intensities (post filter) to the original colour of light (pre filter).
Since an optical interface is being used which can only transfer data digitally there is no way of transferring the 3 analogue voltage values directly to the computer. The PIC is used to sample the 3 values, store them, and then convert them into a form which is analysable by the PC. The way chosen to do this was to take a voltage value (in 8-bit so between 0 and 255), and a time delay proportional to this which turned the output port either on or off after each delay. The code snippet below shows how this was achieved although full code for all programs used in the project can be found in the appendices.
//liner delay subroutine (0xFF times input variable);
a equ 0x45
b equ 0x46
delay movwf a
movlw 0xFF
movwf b
ca movwf b
cb decfszb
goto cb
decfsz a
goto ca
return
The delay loop assumes that the voltage value has previously been stored in a. When the loop is called the embedded loop repeats 256a times, creating a time delay proportional to a. By turning the output port on and off, before and after the loop is called, a square wave output of voltage can be created with a period proportional to the input voltage.
movlw b'00000001'
movwf PORTB
// then call the delay loop
movlw b'00000000'
movwf PORTB
This can be repeated 3 times for each of the measured values, resulting in three flashes. The timed pulses will then be sent optically to the computer.
For documentation on how to program your PIC or other microchip I recommend visiting the manufacturers website at http://www.microchip.com/stellent/idcplg?IdcService=SS_GET_PAGE&nodeId=64
So the image to the right is pretty much a summary of the whole system from

LDR to PIC to LED. After this stage the 3 flashes and their corresponding delays (how long they are on/off for) is sent to the computer via an optical to digital converter.
The final step was to write some software in C (as well as a codec for the optical to digital converter), to output RGB values and display something nice on the screen, in this case a blue LED is being shone onto the LDRs.


Verlet Integration

var previous:Point = (0,0);
var tx:Number = 0;
var ty:Number = 0;
tx = current.x;
ty = current.y;
current.x += (current.x - previous.x + F)*R
current.y += (current.y - previous.y + F)*R
previous.x = tx;
previous.y = ty;Saturday, 12 September 2009
Old physics engine



Friday, 11 September 2009
Buzz - New Game Project
 I'm currently building a new game, so I thought I'd blog at each stage of the way. The game I'm working on is called Buzz and its a game about bees. You control a swarm of bees as they fly around levels trying to pollinate flowers as quickly as possible. I decided to write this game after hearing about colony collapse disorder - a relatively new term given to the phenomenon where bees abandon their hives. The disorder only effects honey bees
I'm currently building a new game, so I thought I'd blog at each stage of the way. The game I'm working on is called Buzz and its a game about bees. You control a swarm of bees as they fly around levels trying to pollinate flowers as quickly as possible. I decided to write this game after hearing about colony collapse disorder - a relatively new term given to the phenomenon where bees abandon their hives. The disorder only effects honey bees