Some incredible renders of the Buddhabrot and Nebulabrot

I'm working on implementing buddhabrot/nebulabrot rendering in the Mandelbrot Explorer application. The buddhabrot - so named because it resembles the classic statue of Buddha - is a more beautiful version of the Mandelbrot, and the Nebulabrot is a slight variation on this.

The idea is that regions that escape the Mandelbrot set are plotted as they head off to infinity. The colour of each point depends on how often that point is seen to head off to infinity. Here are a few images - I can't wait to get a working demo - it does run very slowly in flash at the moment so I'll try and sort that out. Click on the images to expand them!

The nebulabrot uses a rendering Method that is exactly the same as the way false colour is applied to images of the universe by astrophysicists. The resemblance is phenomenal!

Enjoy them and I'll post a flash generator soon!

(Images are: Buddhabrot, Anti-buddhabrot, Nebulabrot, Nebulabrot horizontal)

The Julia Set

If you look at the Mandelbrot Explorer application in my previous post you'll notice a "generate julia set" button on the screenshots.

It turns out that each point on the Mandelbrot Set has an associated Julia Set. The flash app below moves around the complex plane, in a spiralling motion drawing the Julia Sets for each complex location. Just click the image to launch it!

Mandelbrot Explorer

As I've mentioned a few times now I've been working on an application for Windows called "Mandelbrot Explorer". Nothing special, just functional exploration of the mandelbrot and julia sets. This is what 3rd year physicists spend their time doing - a lot of C++!

Here are a few screen shots and an outputted jPeg file. The program is capable of producing high resolution "deep zoom" images of 1200 by 800 pixels. These can look amazing. It handles powers of the mandelbrot set, as well as different forms - including the amazing "Burning Ship" fractal.

Here are a few screenshots.

The classic Mandelbrot Cardiods

The burning ship fractal:

A high res output saved as a low quality jpeg

The Program is free of charge to anyone who wants it. Just send me a note and I'll provide download links! Enjoy the beauty of mathematics.

Augmented Reality - Some examples

Hey everyone - I've been playing around with some of my own augmented reality functions - they don't use the FLAR toolkit - but I plan on looking into this sometime soon!

Here are a few images of what I have so far!

       

I'll post an update with some example files for you to play around with!

Update: put some examples up on the server -

Click here for some simple motion tracking

Click here for green object tracking (you'll need something green and don't wear a green jumper!)

or click here for the 3d monkey head example.

Enjoy!

Strange Attractors - Drawing the universe

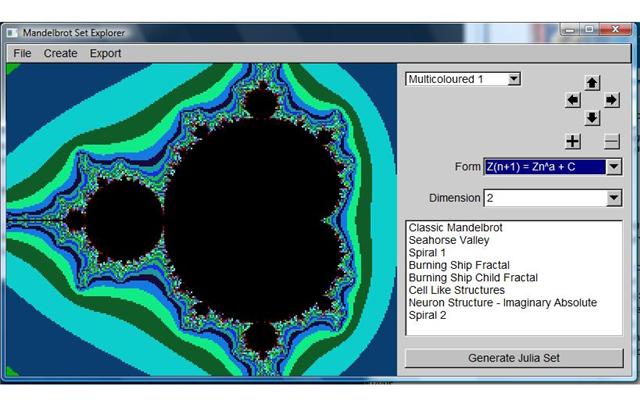
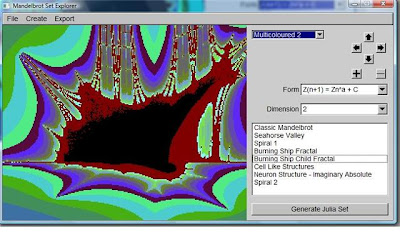
One of my university projects currently involves me writing a Mandelbrot Explorer application, which is yielding some fairly cool results. I've been looking at multiple dimensions and different forms of the mandelbrot set, which just reinforces my amazement every time I run it.

The mandelbrot is a fractal set, so I thought it might be interesting to look at some other fractal sets. Below is a representation of a Strange Attractor - technically a system with chaotic dynamics and a non-integer dimension. The whole program was written in just a few lines of code and it is actually fairly straight forward to work out, just like the Mandelbrot set, but the results are spectacular. It really does seem like the universe is being drawn out in front of you - and it is true that a lot of the patterns found in fractal mathematics do appear in the structures of macroscopic objects, for example in the spiral arms of galaxies, or in nebula cloud formation.

One amazing thing about the program is that there are more possible combinations of what you can see than there are particles in the universe. Current astronomers put the number of particles in the universe at somewhere between 10⁷² and 10⁸⁷a number quite easy to write down. With accurate enough numbers there are infinitely many manifestations of the strange attractor, but practically for an image with 2000x2000 resolution - as the program has, and 256 colours per pixel the number of manifestations are of the order of 256^4000000 which is an incomprehensible figure! And thats just using  256 colours - ie red or green or blue, and not the whole spectrum available.

These numbers are a little bit scary but it is nice to know that some consistency and calm arises out of these. Its not all white noise! Anyway take a look at the program - It is constantly evolving - and you'll never ever see the same thing more than once! Just click the image below to launch it.

Or click here or here to run it in green or blue!

My new game - Match n Slide Aqua preview!

Here are a few screenshots of my new game, a Match3 style game with an underwater theme.

So far I've just been working on the graphics and I'm quite pleased with what I have so far. The first image is the main menu, and the latter is the in game view. Next job, draw some fish! Any feedback would be very much appreciated.

Here's a little update - I'm looking at porting this into an iPhone up as soon as the CS5 beta becomes available, stay tuned!

Love letter to flash

I stumbled across this on youtube. Absolutely amazing! Enjoy! Just click the image below to play the video! Enjoy :)

Fluid Dynamics using AS3

As a physicist I find things like this incredible. Fluids are extremely complex mathematically, so when I came across Eugine Zatepuakin's work on fluid dynamics I was amazed by the speed and accuracy of the simulations!

Just click the right image for a full preview, you'll be blown away! When I've got a bit more time I'll write a thread explaining how fluid dynamics simulations work, and explain the basic principles of coding something like this in flash, but for now check it out!

Move your mouse around to create dense regions and click to change the rendering mode. I love that flash is capable of handling these kinds of calculations. I remember playing a game called plasma pong which used very similar fluid dynamics to Eugine's model. Unfortunately the game is no longer available for download because pong is a trademark of Atari but here is a nice little video of the game in action.

Here is a little youtube clip of the game, just click to launch it! :)

Enjoy!

Flash CS5

I thought I'd just post a quick blog about some news regarding the release of Adobe CS5. Just check out the CS5 blog for a bit more information! Here is a video of Richard Galvan discussing the release, and some of it's features at Flash on the Beach in Brighton last month. Its looking very cool.



Adobe Flash CS5 Viper presented on FOTB 2009! - www.CS5.org from Adobe CS5

While I'm on the topic of Adobe Product Endorsement haha, I thought I'd let you all know about Flash Catalyst. For those of you who aren't programmers but want to get started on some flash based websites or interactive applications, check it out. There is a beta 2 release currently downloadable from the Adobe website, and it looks really good!

Update: Some really big news on CS5 (actual flash, and not catalyst). Instead of just being able to export .swf you will be able to export .ipa! iPhone apps created entirely in flash. This is incredible news!

So excited, waiting for the beta to be released, check out a preview here