HTML5 Mandelbrot Explorer

A simple Mandelbrot explorer for HTML5, in javascript. I plan on optimizing and extending the functionality of the example when I have a bit less uni work to keep up with.

Circle Packing - brute force approach

Earlier this year, as part of my degree, I carried out a project that involved measuring the fractal dimension, and packing densities of various systems. I thought I'd have a play around with something along similar lines, circle packing.

There are many subtle and interesting and above all intelligent ways of packing circles into spaces, but this is not one of them. I decided to take a brute force approach. This is the structure my algorithm took:

• Pick a random point, if it is within any circles that already exist find a new point
• Increase the radius of that point until it overlaps with either the edge of the scene, or another circle on the scene.
• Draw the circle

This is as far as I can tell, both the simplest approach and the slowest. Lets take a look at the results, click the image to run the application. An interesting idea is to draw a line between each circle when they collide. This forms a kind of node based structure between circles, creating a network where larger circles hold more power in the network. I wonder if you could create a page ranking system based on something like this...?

Benoit Mandelbrot - Fractals and the art of roughness

A personal hero of mine talks about fractals.



I enjoyed his quote at the end and found it quite relevant to a lot of the work I do on this blog:

"Bottomless wonders spring from simple rules... repeated without end"

Von Neumann Cellular Automata

I just saw the TED talk from Stephen Wolfram below and noticed I'd never written any 1D cellular automata. He briefly mentions rule 30 and the emergence of complexity from a simple set of rules. The Von Neumann automata is very simple to write. Given a single cell, the state of the new cell (either on or off) is determined by the cells in its local neighbourhood. In one dimension this means the state of itself, the cell just to its left, and the cell just to its right. This means there are 8 possible states for local neighbourhoods (8 rules) and therefore 256 possible outcomes of the system.



As Mr Wolfram mentions in the talk, most of the outcomes are not particularly interesting, some are very plain and some are quite pretty. Below is rule 26, it looks nice but beyond that it is quite a simple rule. Self repetition on a number of different scales is pretty much all it is capable of. Just click the image to launch it.

The next two examples are rule 30 and rule 110 respectively. These are extremely interesting. Rule 30 displays what Wolfram calls "Class 3" behaviour, which is a chaotic and seemingly random, whereas Rule 110 displays "Class 4" behaviour, which is neither completely random nor completely repetitive. The interaction of various local structures is used to prove Universality. Again just click the images to launch the programs!

Rule 30 can be used as an excellent random generator:

Notice the life-like region travelling up near the centre in Rule 110:

Road Generation: First Attempt

I decided to take a look at using Voronoi diagrams to generate road systems. Here are a few very early screenshots! Looks promising.

Inverse Mandelbulb Pixel Mapping in Flash

When we map the 2d Mandelbrot Set we normally colour a pixel depending on the rate at which that point tends to infinity on some colour scale. In 3D normally this wouldn't work - where you have solid objects you'd be changing their colour internally. But since we are looking at cross sections using the voxel renderer it is actually very doable. Here are a few examples:

Remember that the inverse is being mapped. I really like the effect, and its definitely nice to add some colour to the dull grey images of the previous post.

Its like looking into a three dimensional cave of fractal goodness. Another possibility would be to use transparent pixels and change transparency levels. I will give this a go next as it would allow the whole shape to be seen externally, with colour (possibly? we'll see!)  Anyway click here to see all this fractal goodness happening in real time in flash using AS3! Enjoy

Working - 3D Mandelbrot in Flash

Possibly a world first, I don't know, but I can confirm that I have rendered Daniel White's Mandelbulb set using AS3.

The first render is 216 Million voxels (600*600*600) and took about 10 minutes to do.

This is the 8th order of the Mandelbulb (where things start to get interesting from a fractal detail point of view).

First screenshot is half way through the rendering process:

And here is the finished product:

Hopefully soon I'll have a 3D Mandelbrot Explorer ready and working much like the 2d version previously. I'm currently rendering an image 1000x1000x1000 voxels in size (1 Gigavoxel), and I'll add it to this post when it comes out!

edit: here is the gigavoxel render (zoomed in a bit too much though which I'm annoyed about so it cut off the "colosseum" structure at the top!

here is a quick preview of the voxel engine rendering a lower resolution (400x400x400) version.

To zoom in at the moment you'll just have to right click and press "zoom in" but this won't actually zoom in, just give you can enlarged version. Worth doing if you want to see individual voxels though :)

Enjoy!

edit: Just started playing with zooming and rotating:

Here is a view of the colosseum structure (normally at the top) from the side:

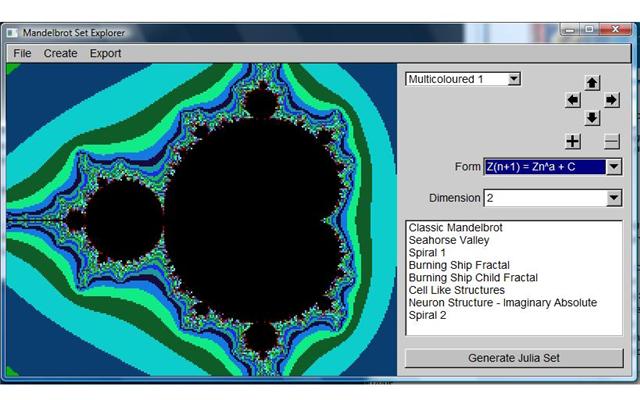
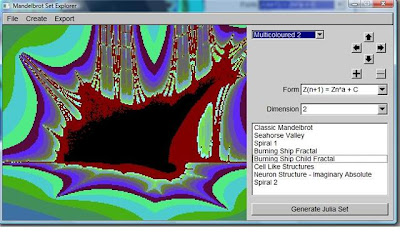
Mandelbrot Explorer

As I've mentioned a few times now I've been working on an application for Windows called "Mandelbrot Explorer". Nothing special, just functional exploration of the mandelbrot and julia sets. This is what 3rd year physicists spend their time doing - a lot of C++!

Here are a few screen shots and an outputted jPeg file. The program is capable of producing high resolution "deep zoom" images of 1200 by 800 pixels. These can look amazing. It handles powers of the mandelbrot set, as well as different forms - including the amazing "Burning Ship" fractal.

Here are a few screenshots.

The classic Mandelbrot Cardiods

The burning ship fractal:

A high res output saved as a low quality jpeg

The Program is free of charge to anyone who wants it. Just send me a note and I'll provide download links! Enjoy the beauty of mathematics.